Metre Bridge - Special Case of Wheatstone Bridge

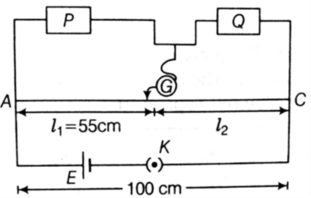
In a meter bridge balance point is found at a distance  $l_1$  with resistances R and S as shown in the figure.



When an unknown resistance X is connected in parallel with the resistance S, the balance point shifts to a distance $l_2$ . Find the expression for X in terms of  $l_1$ ,  $l_2$  and S.

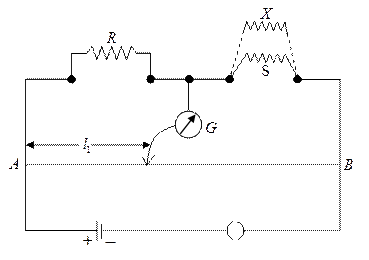
In a meter bridge experiment, resistances are connected as shown in figure. The balancing length $l_1=\; 55 \mathrm{cm}$. Now, an unknown resistance $\frac{n}{11} \mathrm{\Omega }$ is connected in series with $P$ and the new balancing length is found to be $75\mathrm{ }\mathrm{cm}$ . The value of $n$ is (Given, $P=4 \mathrm{\Omega }$ )

How do you find the resistance of a wire using a meter bridge?

What is balance point in Kelvin's method of determination of galvanometer resistance Shaalaa?

What is the use of Kelvin's method?

What is the use of Kelvin's method?

What are the applications of meter bridge

Why meter bridge is not suitable?

What is meter bridge?

What are the limitation of Metre bridge?

On interchanging the resistances, the balance point of a meter bridge shifts to the left by $10 \mathrm{cm}$10 cm. The resistance of their series combination is $\mathrm{1 }\mathrm{k\Omega }$ . How much was the resistance on the left slot before interchanging the resistances?

In a meter Bridge experiment resistance $x$ is connected in the right gap. When $R_1$ and $R_2$ are connected in the left gap separately the balance points are $40\mathrm{ }\mathrm{c}\mathrm{m}$ and $50\mathrm{ }\mathrm{c}\mathrm{m}$ respectively from the left end. Now if both $R_1\mathrm{ }\&\mathrm{ }{R}_2$ are connected in series in the left gap with $x$ in the right gap the new balance point from the left end (in $\mathrm{cm}$) is $l^{\text{'}}$, what is the value of $2l^{\text{'}}$?

The circuit diagram given in the figure shows the experimental setup for the measurement of unknown resistance by using a meter bridge. The wire connected between the points $P \& Q$ has non-uniform resistance such that resistance per unit length varies directly as the distance from the point $P.$ Null point is obtained with the jockey $J$ with $R_1$ and $R_2$ in the given position. On interchanging the positions $R_1$ and $R_2$ in the gaps the jockey has to be displaced through a distance $\Delta$ from the previous position along the wire to establish the null point. If the ratio of $\frac{R_1}{R_2}=3,$ find the value of $\Delta$ (in $cm$). Ignore any end corrections. [Take $\sqrt{3}=1.7$]

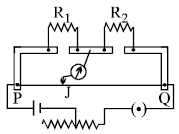
In the given meterbridge, $AB$ is a wire of uniform cross-section and its resistivity changing from $A$ to $B$ as $\rho ={\rho }_0\frac{x}{\ell }$. If deflection in galvanometer is zero at $P$ such that $x=\frac{\ell }{\sqrt{\alpha }}$, the value of $\alpha$ is.

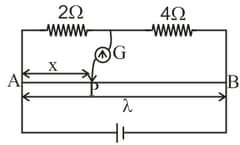
Figure shows a Meter bridge wire $AC$ has uniform cross-section. The length of wire $AC$ is $100 \mathrm{cm}$ $X$ is a standard resistor of $4 \mathrm{\Omega }$ and $Y$ is a coil. When $Y$ is immersed in melting ice the null point is at $40 \mathrm{cm}$ from point $A$. When the coil $Y$  is heated to $100°\mathrm{C},$ a $12 \mathrm{\Omega }$ resistor has to beconnected in parallel with $Y$ in order to keep the bridge balanced at the same point. The temperature coefficient of resistance of the coil is $x\times {10}^{-2} \mathrm{SI}$ units. Find the value of $x$.

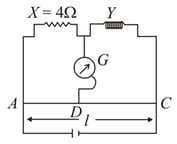
Consider the meter bridge circuit without neglecting end corrections. If we used $100 \mathrm{\Omega }$ and $200 \mathrm{\Omega }$ resistance in place of $R$ and $S$ respectively, we get null deflection at $l_1=33.0 \mathrm{cm}$. If we interchange the resistances, the null deflection was found to be at $l_2=67.0 \mathrm{cm}$. If $\alpha$ and $\beta$ are the end correction, then the value of $\alpha +\beta$ should be

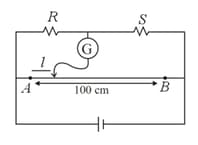
If the wire in the experiment to determine the resistivity of a material using metre bridge is replaced by copper or hollow wire the balance point i.e. null point shifts to

Null method is superior over deflection method because

Where do we get the balancing point of the meter bridge generally?

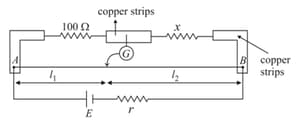
In a practical meter bridge circuit as shown, when one more resistance of $100 \mathrm{\Omega }$ is connected in parallel with unknown resistance $x$, then ratio $\frac{l_1}{l_2}$ become $2$. $l_1$ is balancing length.$AB$ is a uniform wire. Then value of $x$ must be: